塾(日能研)の予定表が毎月、印刷物で配られます。 あるいは、マイページからpdf形式でダウンロードできます。

いずれにせよ、それらをカレンダーに手動で登録するのが面倒臭い
もう一つ言うと、高学年の予定の日付を確認するためには視線をいちいち左右に振らないといけないので辛い
ということで、OCRを使ってイベントを抽出し、Googleカレンダーに登録するということをやってみました。
OCRの認識精度(テキスト区切りの安定さも含めて)が完璧ではないので、全自動ではなく半自動のシステムになりますが一応やりたいことはできるようになりました。
全体の構成
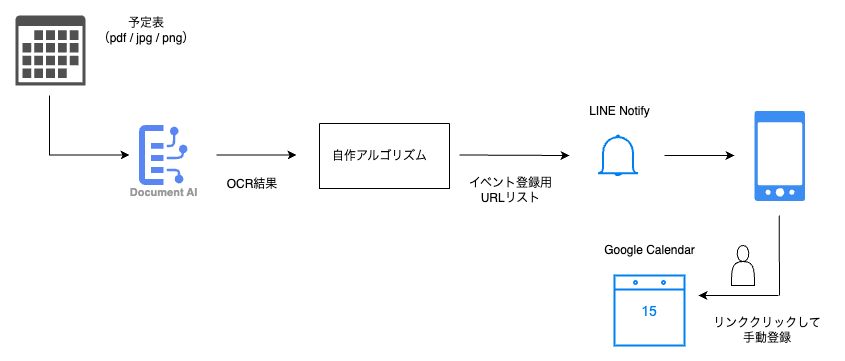
OCRで抽出したテキストから必要な情報を取り出し整形し、LINE Notifyにてスマホに通知します。
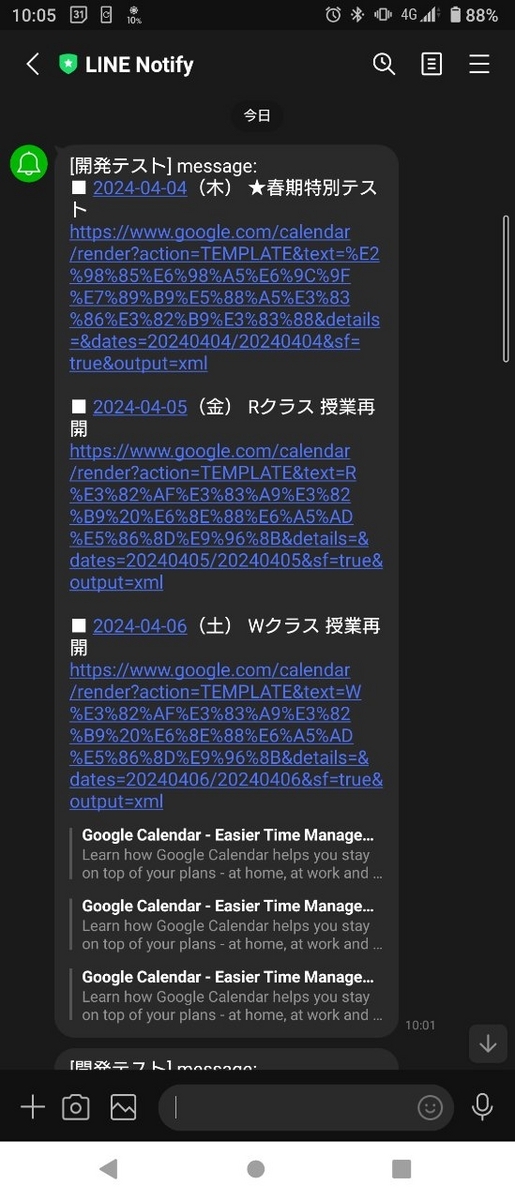
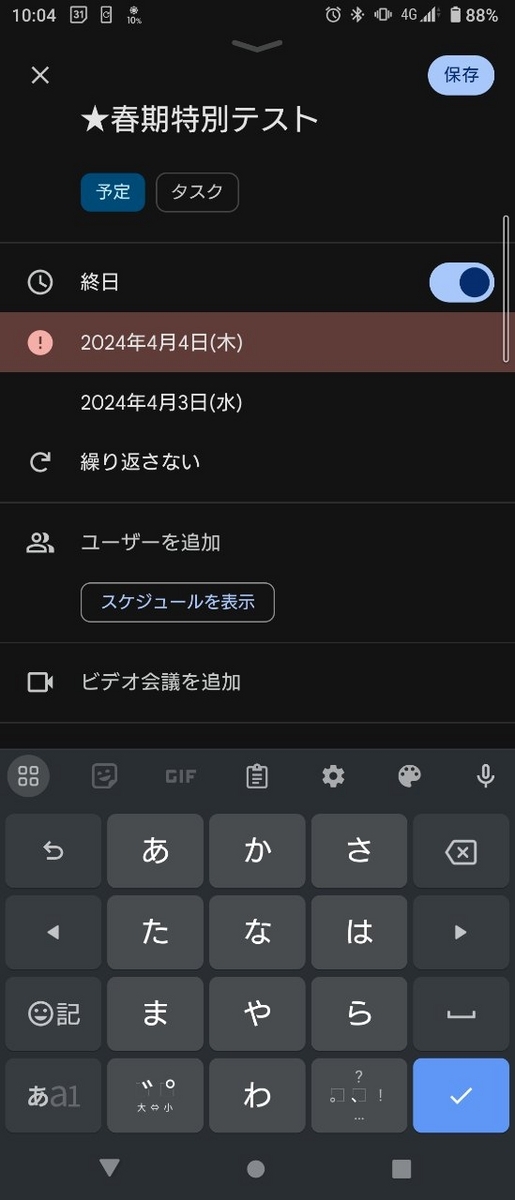
Googleカレンダー登録用のURLを作成して通知するだけなので自動でスケジュール登録はできません。
ただ、イベント情報の抽出が一部間違っていたとしても、カレンダー登録時に修正が手動で可能なので正確性は担保できるし、手間は十分に省けます。 また、手動登録にすることで自分のクラスに関係ないイベントもフィルタリングできます。
OCR
GCPのDocument AIを使いました。 Cloud Vision APIでもOCRでテキスト抽出できるのですが Document AIは情報をテーブル構造で抽出できるForm Parserというのがあり、Document AIを選択しました。
ただ、今回対象としている予定表は部分的な入れ子構造があったり、複数セルに覆いかぶせる形でのテキスト重畳があったり、複雑な表になっているので実際にはテーブル構造での情報抽出はうまくいきませんでした

ということで、Document AI を使ってますが通常のOCRプロセッサによる処理です。
Document AIではローカルのpdfファイルも扱えますがCloud Vision APIでは(現時点では)Cloud Storage上のpdfファイルしか扱えないようで、システム面ではダウンロードしたpdfファイルをダイレクトに処理できるDocument AIのほうが地味に好ましいです。 (Cloud Vision APIの場合、pdfを画像化すればローカルのファイルでも問題ないです)
公式ページ では以下のようにDocument AIとCloud Vision APIのユースケースについて記述されています。

Document AIのコスト
Cloud Vision APIは最初の1000オペレーション/月は無料です。 一方、Document AI は無料枠がありません。。
公式ページ の料金表によると 1,000 ページあたり $1.50 となっています。
1ドル155円として、1ページあたり 1.5 / 1000 * 1 * 155 = 0.2325円
大量の枚数を処理しない限りはそこまで気にする料金ではないと思ってますが無料でできるのに越したことはないのでCloud Vision APIのOCRに乗り換えられるか、今後試してみようと思います。
ちなみに、テーブル構造で抽出できるFormパーサーだと1,000ページあたり $30 となり、通常のOCRプロセッサの20倍するのでコストにはある程度気を配る必要があります。
抽出アルゴリズム
抽出アルゴリズムの概要は以下の通りです。
- 日付に相当するテキスト群を抽出し、そのおおよそのx座標を計算する
- 対象学年のテキストを抽出し、その学年のイベントに相当するx座標を計算する
- 学年のイベントと思われるテキストを抽出する
- イベントテキストのy座標にマッチする日付を抽出する

ゴリゴリと日能研の予定表に特化したルールベースでやっているので残念ながら他のフォーマット(スケジュール表)には対応できず、拡張性がありません..。 日能研にしても、他校の予定表に対して適応できるかはわかりません。。
当初の目論見通りにFormプロセッサを使ってテーブル構造でばっちり情報抽出できればカラム定義表のカスタマイズ程度で他の予定表にも対応できるはずなのですが残念です。
使ってみて
スマホでさくっと塾の予定確認できる状態になったのは非常に便利です。
OCR&予定抽出のアルゴリズムの精度が十分であればLINEに通知するだけでも十分有用かなと感じました。 (現状だと間違った日付になってしまったり、イベントの漏れがある可能性があるので若干危険)






























