Karpathy先生のCS231nの講義スライドも使いつつ覚えておきたいポイントをまとめてみます。
畳み込み(Convolution)のイメージ図
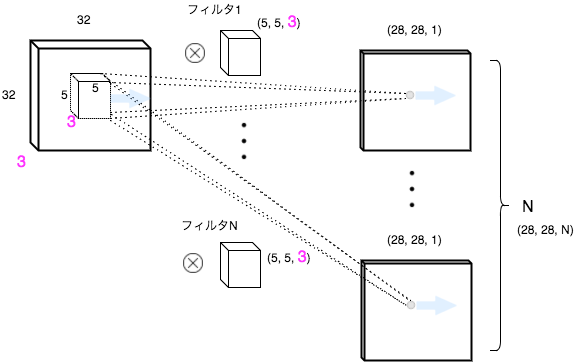
ポイント
- 入力のdepthとフィルタのdepthは同じ。フィルタを適用して1つの値を出力
- フィルタをスライドさせながら適用して 1枚の アクティベーションマップを 出力
- N枚のフィルタから N枚のアクティベーションマップを 出力
畳み込みの演算
F = フィルタサイズ
np.sum(X[x:x+F, y:y+F, :] * W) + b
- フィルタサイズで切り取った X に W を elementwise掛け算 して
- 演算結果をすべて足し込んでさらに bias を足す
別の書き方をすると
np.dot(X[x:x+F, y:y+F, :].flatten(), W.flatten()) + b
とも書ける。
ネットワーク全体のイメージ図
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
- N: 0 ~ 3程度
- M: 0 ~
- K: 0 ~ 3程度
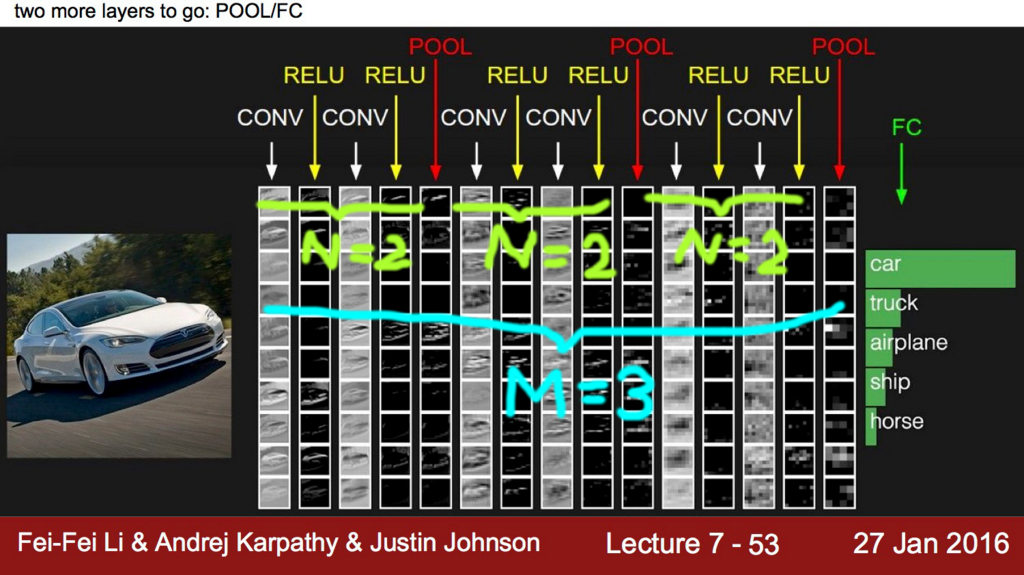
CONV層 + RELU層 と POOL層を重ねて 高次元の特徴を 複数抽出し、全結合(FC)レイヤで 各特徴の重みを学習する というイメージです。
覚えておきたい計算式
アクティベーションマップのサイズ
( W − F + 2P ) / S +1TensorFlowの padding=‘same'は
P=ceil(F/2)、padding='valid'はP=0です。正確な定義はこちらです。パラメータ数
( F * F * 入力フィルタ数 + 1) * 出力フィルタ数+1 は bias項になります。
必要なメモリサイズ
( W * H * フィルタ数 ) * 4 (=float32) バイトバッチサイズはGPUのメモリサイズに依存します。(GPUのメモリ上にのる限りは大きくしたほうがよい)
VGGNetの場合だと
- 画像1枚あたり 93 M (backwardもいれると x 2) となるようです。。
なぜディープにするのがよいのか?
7x7フィルタを1回適用した場合と3x3フィルタを3回適用した場合を比較してみます。
| イメージ | パラメータ数 | |
|---|---|---|
| 7x7フィルタを1回 |  |
(7 * 7 * 3 + 1) * 3 = 444 |
| 3x3フィルタを3回 |  |
(3 * 3 * 3 + 1) * 3 * 3 = 252 |
出力アクティベーションマップのサイズは 26 x 26 で同じですが3層に積み重ねるほうがより大きな表現力があり(非線形処理を3回適用するので)、またパラメータ数も少なくなり学習効率がよくなります。
一方でメモリサイズはより必要になってくるのでトレードオフの関係にはなります。 GPUのスペックが向上することでよりディープに学習することが可能になったと言えるでしょう。
どんどんディープになっていくトレンドですが ILCVRC'15の勝者の ResNet は なんと.. 152層 です。 w|;゚ロ゚|w
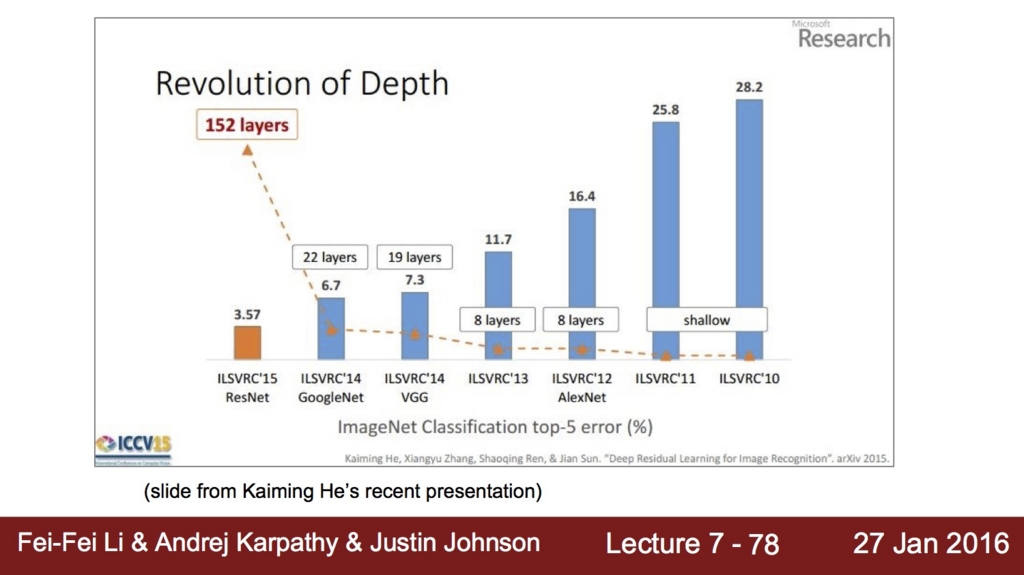
なぜCNNは成功しているのか?
次のような理解で大体あっていると思う。。
画像認識に適したアーキテクチャ
- 畳み込み: 何層も畳み込むことで高次元の抽象的な特徴を抽出できる
- プーリング: 位置のずれにロバストになる
以下の2つの大きな課題があったが解決された
- 過学習 (Overfitting)
- 勾配消失問題 (Vanishing gradient problem)
解決の要因
- 手法の進化
- ReLU: 深いネットワークでも勾配が逆伝搬できるようになった
- Dropout: 擬似的にアンサンブル学習することで汎化性能が上がり過学習を抑制できるようになった
- ハードウェアの進化(特にGPU)
- 大量のデータ、大量のパラメータを処理できるようになった
勾配降下法(gradient descent)の実装サンプル
1次元データでCNNのgradient descentをNumpyで実装してみました。 スクラッチで実装すると少し自信がつく気がします。。 (o・ω・o)
今回は以上です。次は RNN の記事を書いてみようと思います。